Context-Free Grammar (CFG) is a set of production rules that describe all possible strings in a given formal language. For example;
A → x
A → y
B → z
With these defined rules, we can replace A with 'x' or 'y' ; B with 'z' for output. Context-Free Grammar G is defined by the 4 value;
V = In grammer rules, this shows the elements named "variables" where be on the left side of grammer arrows. Variables are not include in our outputs. For our example V={A,B}.
T = In grammer rules, this shows the elements named "alphabet" where be on the right side of grammer arrows. We create the output with these elements. For our example T={x,y,z}.
P = This symbolize set of Grammer rules.
S = This indicate the Start State. Start state shows us to which rule or rules we have to use to apply the grammer rules. For our example S={A}.
Let's use these with example
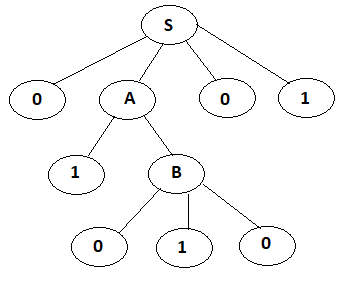
S → 0A01
A → 1B
B → 010
Let's start with determination of these gammer G's values;
V = {S , A , B} T = {1 , 0} S = {S} ===> G=({S , A , B} , {1 , 0} , P , {S})
Now we can generate out output. For example we can generate this output with given grammer rules;
S → 0A01 → 01B01 → 0101001
For understand better, we can represent example with Derivation Tree.

E → E + E
E → E * E
E → number
This example's grammer rules make addition and multiplication. Let's assume the E = 2*3+4 and when we apply the grammer rules to E, it will be accepted.
Let's try to draw this example's derivation tree:
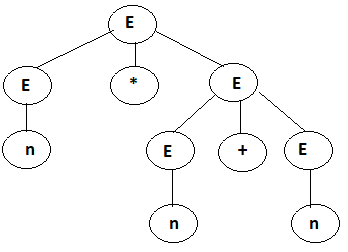
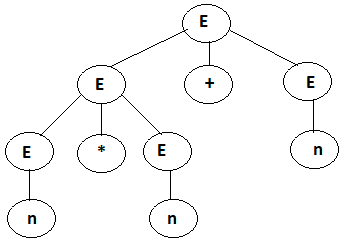
As you can see, with this grammer rules, we can draw more than one derivation trees. This situation called a Ambigous. We need to add some variables to solve this problem. When we add some variables to grammer rules, this derivation trees can not be same.
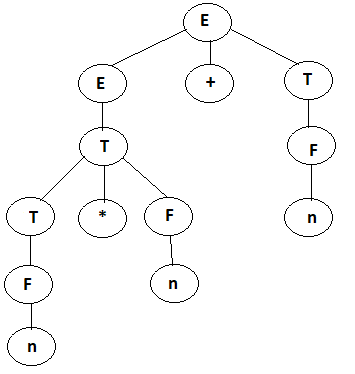
E → T | E + T
E → F | T * F
F → number
Now we can draw a derivation tree of this rules.
E → T | E - T
E → F | T / F
F → number | ( E )
In this example, you can try the grammer rules via program. With given Expression, you can examine how grammer rules work.
1) https://www.wikiwand.com/en/Context-free_grammar
2) Above examples what we work on, derived from examples in Automata Theory lesson's laboratory studies.