Context Free Grammar

Definition − A context-free grammar (CFG) consisting of a finite set of grammar rules is a quadruple (N, T, P, S) where

N is a set of non-terminal symbols.

T is a set of terminals where N ∩ T = NULL.

P is a set of rules, P: N → (N ∪ T)*, i.e., the left-hand side of the production rule P does have any right context or left context.

S is the start symbol.

Example:

The grammar ({A}, {a, b, c}, P, A), P : A → aA, A → abc.

The grammar ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε

The grammar ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε

Summary

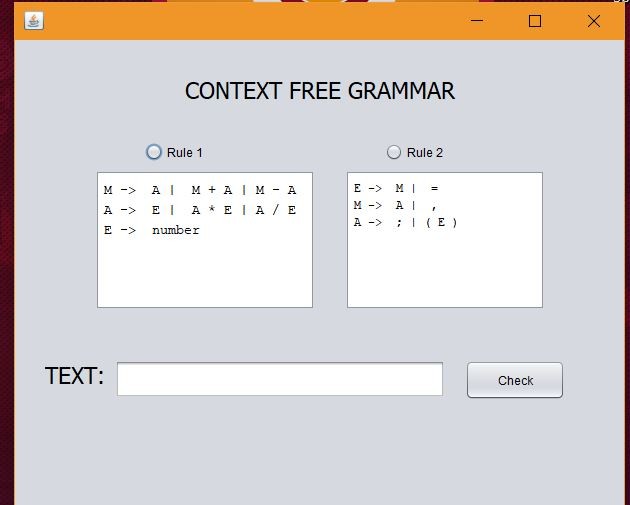
Firstly user selects one of the above rules and if the user writes a text,the accuracy is measured according to the selected rule.
The result seens on the screen as accept or reject.

Project Topic

According to the rule selected by the user, the entered text must be checked accept or reject.

Project Content

Program Errors:

As I have seen above, I have set two rules in CFG. Below, the program alerts the user.

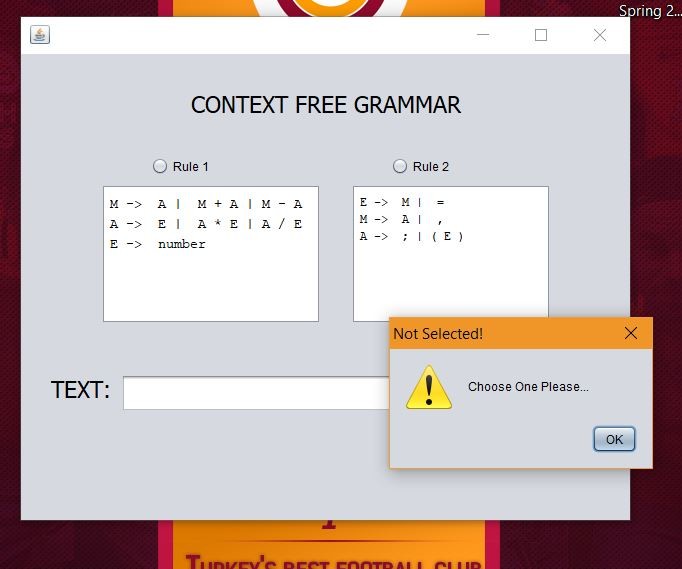
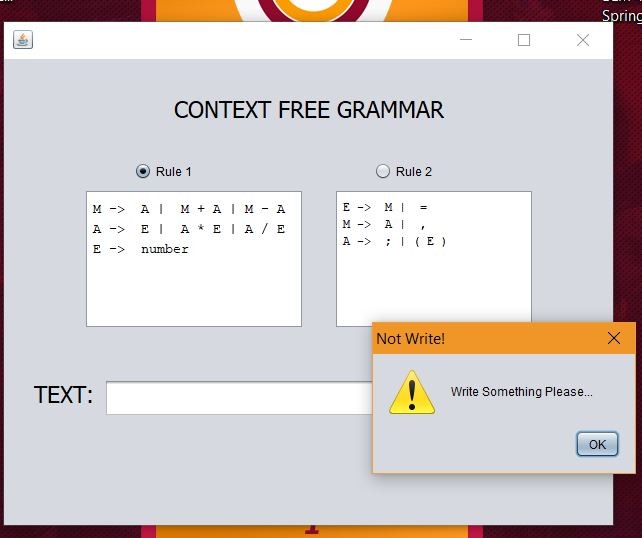The user is redirected according to this error.

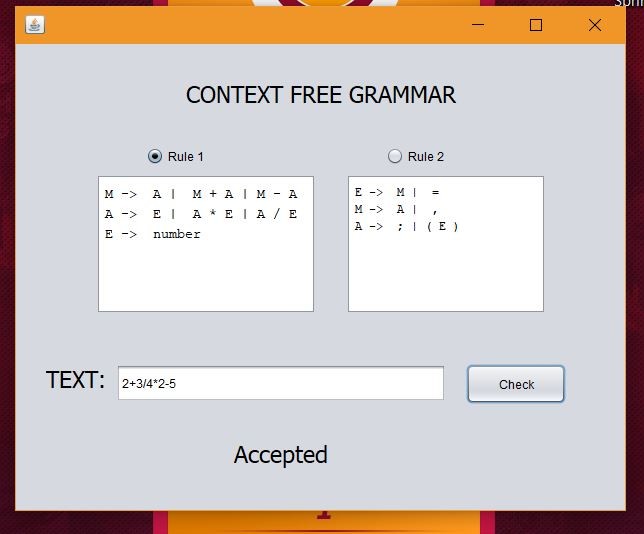
Rule 1:

M -> A | M + A | M - A
A -> E | A * E | A / E
E -> number

Rule 1 only accepts four operations and numbers in mathematics.

Example for accept;

M = 2*4+7-5/3

When Rule 1 is selected, it is shown below in the form of accept and reject.

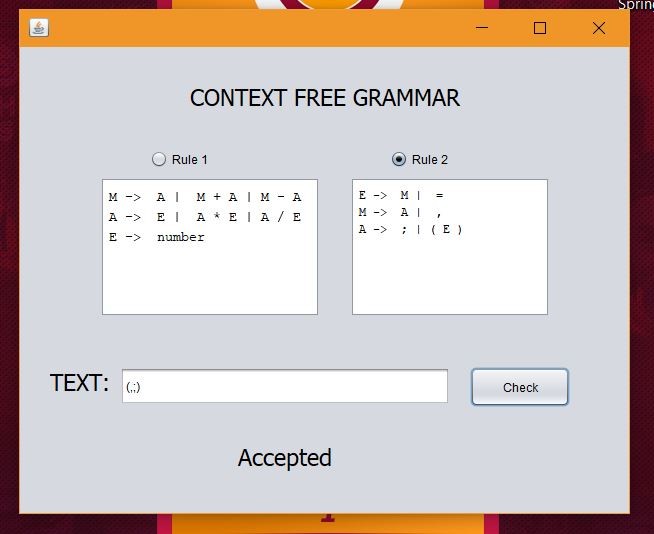
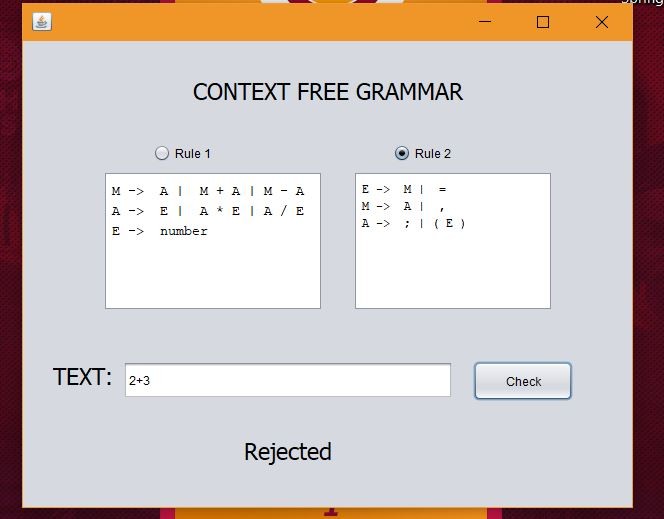
Rule 2:

E -> M | =
M -> A | ,
A -> ; | ( E )

Rule 2 accepts special characters. It does not accept mathematical expressions.

Example for accept;

E = (=,;)

Similar images are found in Rule 2 below.

REFERENCES:

https://www.tutorialspoint.com/automata_theory/context_free_grammar_introduction.htm