Automata-2018
NFA TO DFA CONVERTER
In DFA, for each input symbol, one can determine the state to which the machine will move. Hence, it is called Deterministic Automaton. However all the state to the NFA is unclear.
DFA and NFA definition Q=states
∑=input alphabet
δ=transition function δ: Q × ∑ → Q
F=final state F ⊆ Q
S=start state S ⊆ Q
Note:
- The initial state is denoted by an empty single incoming arc.
- The final state is indicated by double circles.
Example 1
Convert the following nfa to dfa.
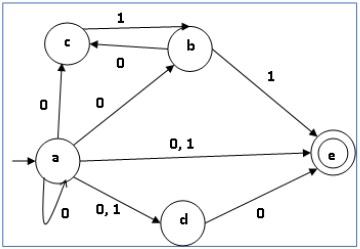
Convert the following nfa to dfa NFA
| δ | 0 | 1 |
|---|---|---|
| -> a | {a,b,c,d,e} | {d,e} |
| b | {c} | {e} |
| c | ∅ | {b} |
| d | {e} | ∅ |
| *e | ∅ | ∅ |
We need to figure out where to go for each state. NFA -> DFA
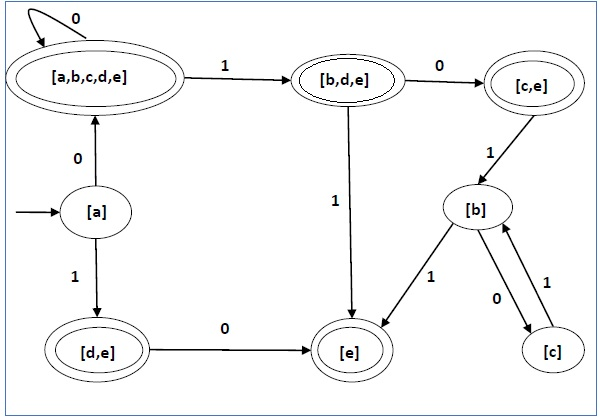
| δ’ | 0 | 1 |
|---|---|---|
| -> a | a,b,c,d,e | d,e |
| *a,b,c,d,e | a,b,c,d,e | b,d,e |
| *d,e | e | ∅ |
| *b,d,e | c,e | e |
| *e | ∅ | ∅ |
| *c, e | ∅ | b |
| b | c | e |
| c | ∅ | b |
Nfa ends in e state. Every state goes to e for dfa.
Drawing the dfa chart:
Example 2
NFA Convert nfa to regex to dfa. Regex : (0+1)*10
1 or 0 may come. 1 and 0 have to come

This nfa table:
| δ | 0 | 1 |
|---|---|---|
| ->q0 | {q0} | {q0,q1} |
| q1 | {q2} | ∅ |
| *q2 | ∅ | ∅ |
NFA -> DFA
| δ’ | 0 | 1 |
|---|---|---|
| ->q0 | q0 | q0,q1 |
| q0,q1 | q0q2 | q0,q1 |
| *q0q2 | q0 | q0,q1 |
This table drawing:
DFA

Java Application
In my application, it is checked whether the appropriate string is entered in the table.

If we draw the diagrams here we can see input will be accepted by this regular expression. Start and final states is known before starting to processing for each input.
Java Project : here

It is reject not suitable for Regex.
DFA and NFA are shown step by step through which states they pass. At the very end it says it is accepted or rejected.
References For Examples:
https://www.tutorialspoint.com/automata_theory/images/ndfa.jpg
https://www.tutorialspoint.com/automata_theory/images/dfa_state_diagram.jpg
This page made by Selin Daldaban