


Q : Finite set of states.
∑ : set of Input Symbols.
q : Initial state. It is the starting state of a machine
F : set of Final States.
δ : Transition Function. It is defined as δ : Q X ∑ --> Q.
Default deterministic finite automaton consists of:
A = (Q,Σ, δ, q0,F)
In a DFA, for an input character, machine goes to one state only. A transition function is defined on every state for every input symbol.
In Deterministic model of Finite Automate (DFA): for every possible combination of state (Q) and language symbol (Σ), we always have unique next state.

1. We start with the initial(start) state of the DFA, q0.
2. By using the transition function δ, suppose that δ(qO,a1) == q1 then the next state will be q1.
3. Until we find final state(maybe we won't find the final state), we will continue to use transition functions. Suppose that δ(q1,a2) == q2
4. If we find the final state in given string then we accept the string.

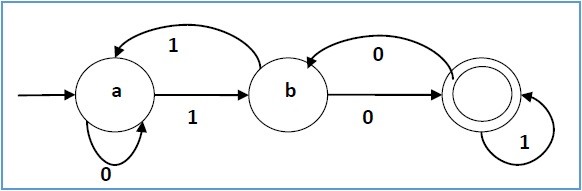
Based on the representation of the DFA:
Q = {a, b, c}
Σ = {0, 1}
q0 = {a}
F = {c}
The transition table should like the the following
| Present State | Next State for Input 0 | Next State for Input 1 |
|---|---|---|
| a | a | b |
| b | c | a |
| c | b | c |
This website is designed by Ebrar SAHIN.
Technologies:
1. JavaScript --> JQuery: used for actions and algorithms
2. HTML: used for website
3. Sketch: used for UI design
References:
1. https://stackoverflow.com/questions/15617429/ambiguity-in-transition-how-to-process-string-in-nfa
2. https://www.tutorialspoint.com/compiler_design/acceptability_of_a_string_by_dfa.asp
As I mentioned above, We need some information about DFA. As a result,
1. We need to give information about initial and final state for the first step of my program.
2. For the accepting and rejecting string, we need to give information about transition function.
3. For the final stage of my program, we need to give a string to check if our string is accepted or rejected
by using our transition function.
Note that my program has 3 states.