FINITE AUTOMATA

A finite automaton (FA) is a device that recognizes a language (set of strings). It has finite memory and an input tape; each input symbol that is read causes the machine to update its state based on its current state and the symbol read. The machine accepts the input if it is in an accept state at the end of the string; otherwise, the input is rejected.
The finite automata's special type shall include the following 3 states:
In all cases (State) the condition to be taken is not a single state. In other words, in one case, you can go to one state only with one word.
For any input, accepting a single final state (multiple end states not being considered the same).
Epsilon term does not take place between states.

A Finite Automata consists of the following :
Q : Finite set of states.
∑ : set of Input Symbols.
q : Initial state.
F : set of Final States.
δ: Transition Function.

Formal specification of machine is
{ Q, ∑, q, F, δ }.

FA is characterized into two types:

The state in which the deterministic end state machines are to be included (that is, passed) for each input symbol is determined.
DFA consists of 5 tuples {Q, ∑, q, F, δ}. According to this definition;

Q : set of all states.
∑ : set of input symbols. ( Symbols which machine takes as input )
q : Initial state. ( Starting state of a machine )
F : set of final state.
δ : Transition Function, defined as δ : Q X ∑ --> Q.

The following figure shows the state diagram of a deterministic finite automaton (DFA),

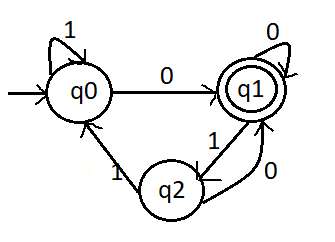
The automaton has three states q0, q1, and q2. The state q0 is the start state and q1 is an accept state. The directed edges between states specify the transitions of the automaton when reading an input string. This automaton accepts the set of strings that contain 1 and have an even number of 0’s after the last 1.

DFA transition table

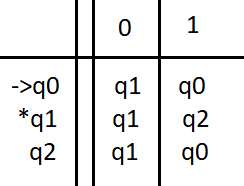
The -> indicates the start state: here q0
The * indicates the final state(s) (here only one final state q1)

For this example:

Q = {q0,q1,q2}

∑ = {0,1}

q = {q0}

F = {q1}

δ = Q X ∑ --> Q

δ(q0,1)=q0
δ(q0,0)=q1

Accepting or Rejecting According to DFA

Transition diagram:

Transition table:

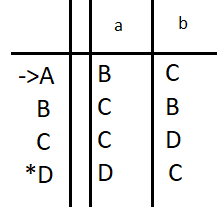
Q={A,B,C,D},∑={a,b},start state A, final state {D}

For this example here is the values:
States: ABCD , terminals: ab, initial state: A, final state: D, transition table: BCCDCBDC, input string: bab --> accept
This values input type you can use for this java program or what you want like this:

download dfa program

2) Non-deterministic Finite Automata (NFA)

An NDFA can be represented by a 5-tuple (Q, ∑, δ, q0, F) where -

Q is a finite set of states.
∑ is a finite set of symbols called the alphabets.
δ is the transition function where δ: Q x ∑ --> 2^Q
(Here the power set of Q (2^Q) has been taken because in case of NDFA, from a state, transition can occur to any combination of Q states)
q0 is the initial state from where any input is processed (q0 ϵ Q).
F is a set of final state/states of Q (F ⊆ Q).